- ТОМ1
- Общетехнические сведения
- Материалы
- Шероховатость поверхности
- Допуски и посадки
- Конструктивные элементы
- Крепежные изделия
- Стандартные и нормализован-
ные детали и узлы - Защитные и защитно-декортив-
ные покрытия металлов
- ТОМ2
- Оси и валы
- Подшипники
- Муфты
- Зубчатые
и червячные передачи - Цепные передачи
- Ременные передачи
- Винтовые передачи
и храповое зацепление - Шариковые винтовые
передачи - Разъемные соединения
Конические зубчатые передачи
Конические зубчатые передачи с прямыми зубьями
Прямозубые конические передачи выполняют с осевой формой I с пропорционально понижающимися зубьями рис. 28) и постоянным радиальным зазором по ширине зубчатого венца.
При обработке зубчатых колес зубострогальными резцами дно впадины имеет коническую форму (рис. 29, a), а при обработке парными зуборезными головками — вогнутую (рис. 29, б).
Числа зубьев шестерни и колеса ортогональной конической зубчатой передачи при исходном контуре по ГОСТ 13754—81 следует выбирать с учетом данных, приведенных в табл. 67.
Число зубьев цементованных конических зубчатых колес рекомендуется определять по номограмме, приведенной на рис. 30.
Термически улучшенные конические зубчатые колеса можно выполнять с тем же увеличенным числом зубьев на 10-20 %.
Модули. В качестве расчетного принят внешний окружной модуль me. Модуль me рекомендуется устанавливать по ГОСТ 9563-60.
Параметры исходного контура. Конические передачи с прямыми зубьями общего назначения при т, выше 1 мм должны выполняться в соответствии с исходным контуром по ГОСТ 13754—81 со следующими параметрами:
a=20°; h*a = 1; с* = 0,2 и р*f = 0,3
Исходный контур для прямозубых конических колес см. на рис. 1.
Выбор коэффициентов смещения и коэффициентов изменения расчетной толщины зуба исходного контура.
1. При и > 1 шестерню рекомендуется выполнять с положительным смещением (х1) по табл. 68, а колесо с равным ему по величине отрицательным смещением (x2 = - x1).
Для передач, у которых и и z1 отличаются от указанных в табл. 68, коэффициенты смещения принимают с округлением в бoльшую сторону.
2. При и ≥ 2,5 зубчатые колеса рекомендуется выполнять не только со смещением, устанавливаемым по п. 1, но и с различной толщиной зуба исходного контура: увеличенной по сравнению с расчетной (πme)/2 у исходного контура шестерни и соответственно уменьшенной у исходного контура колеса.
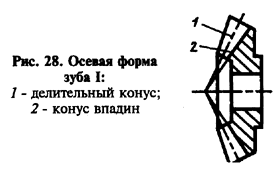
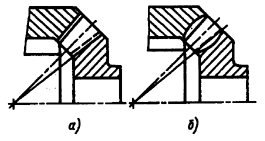
Рис. 29. Форма впадины:
a- при обработке зубострогальными резцами;
б - при обработке парными зуборезными головками
Коэффициент изменения расчетной толщины зуба исходного контура xτ1, положительный для шестерни и равный ему по величине, но обратный по знаку xτ2 для колеса, рекомендуется вычислять по формуле
xτ1 = 0,03+0,008(u-2,5)
67. Минимальное допустимое число зубьев ортогональной конической передачи с прямыми зубьями
| Число зубьев шестерни z1 |
Наименьшее число зубьев сопряженного колеса z2 |
Число зубьев шестерни z1 |
Наименьшее число зубьев сопряженного колеса z2 |
| 12 | 30 | 15 | 19 |
| 13 | 26 | 16 | 18 |
| 14 | 20 | 17 | 17 |
68. Коэффициенты смещения для ортогональных конических зубчатых передач
с прямыми зубьями при исходном контуре по ГОСТ 13754—81
|
Число зубьев |
Значения коэффициента смещения x1 при передаточном числе передачи u |
|||||||||||
|
1 |
1,12 |
1.25 |
1,4 |
1,6 |
1,8 |
2,0 |
2,5 |
3,15 |
4,0 |
5,0 |
6,3 |
|
|
12 |
|
— |
— |
— |
— |
— |
— |
0,50 |
0,53 |
0,56 |
0,57 |
0,58 |
|
13 |
— |
— |
— |
— |
— |
— |
0,44 |
0,48 |
0,52 |
0,54 |
0,55 |
0,56 |
|
14 |
— |
— |
— |
0,27 |
0,34 |
0,38 |
0,42 |
0,47 |
0,50 |
0,52 |
0,53 |
0,54 |
|
15 |
— |
— |
0,18 |
0,25 |
0,31 |
0,36 |
0,40 |
0,45 |
0,48 |
0,50 |
0,51 |
0,52 |
|
16 |
— |
0,10 |
0,17 |
0,24 |
0,30 |
0,35 |
0,38 |
0,43 |
0,46 |
0,48 |
0,49 |
0,50 |
|
18 |
0,00 |
0,09 |
0,15 |
0,22 |
0,28 |
0,33 |
0,36 |
0,40 |
0,43 |
0,45 |
0,46 |
0,47 |
|
20 |
0,00 |
0,08 |
0,14 |
0,20 |
0,26 |
0,30 |
0,34 |
0,37 |
0,40 |
0,42 |
0,43 |
0,44 |
|
25 |
0,00 |
0,07 |
0,13 |
0,18 |
0,23 |
0,26 |
0,29 |
0,33 |
0,36 |
0,38 |
0,39 |
0,40 |
|
30 |
0,00 |
0,06 |
0,11 |
0,15 |
0,19 |
0,22 |
0,25 |
0,28 |
0,31 |
0,33 |
0,34 |
0,35 |
|
40 |
0,00 |
0,05 |
0,09 |
0,12 |
0,15 |
0,18 |
0,20 |
0,22 |
0,24 |
0,26 |
0,27 |
0,28 |
|
Примечание. Данные таблицы могут быть использованы также для повышающих передач при u < 1. |
||||||||||||
69. Ширины зубчатых конических венцов в зависимости от de2 и u
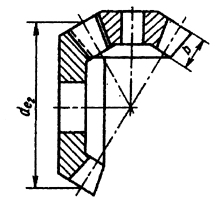 |
Допускается применять ширины зубчатых венцов, определяемые |
||||||||||||||||
| Номинальные значения внешнего делительного диаметра колеса de2, мм |
Ширина зубчатых венцов b, мм, для номинальных передаточных чисел u | ||||||||||||||||
| 1,00 | (1,12) | 1,25 | (1,40) | 1,60 | (1,80) | 2,00 | (2,24) | 2,50 | (2,80) | 3,15 | (3,55) | 4,00 | (4,50) | 5,00 | (5,60) | 6,30 | |
|
50 |
10 |
9,5 |
9 |
9 |
8,5 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
|
(56) |
11 |
10,5 |
10 |
10 |
9,5 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
|
63 |
13 |
12 |
11,5 |
11 |
10,5 |
10 |
10 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
|
(71) |
14 |
14 |
13 |
12 |
12 |
11,5 |
11,5 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
|
80 |
16 |
15 |
15 |
14 |
13 |
13 |
13 |
12 |
12 |
— |
— |
— |
— |
— |
— |
— |
— |
|
(90) |
18 |
17 |
16 |
16 |
15 |
15 |
14 |
14 |
14 |
— |
— |
— |
— |
— |
— |
— |
— |
|
100 |
20 |
19 |
18 |
18 |
17 |
16 |
16 |
16 |
15 |
15 |
15 |
— |
— |
— |
— |
— |
— |
|
(112) |
22 |
21 |
20 |
20 |
19 |
18 |
18 |
17 |
17 |
17 |
17 |
— |
— |
— |
— |
— |
— |
|
125 |
25 |
24 |
22 |
22 |
21 |
20 |
20 |
19 |
19 |
19 |
19 |
19 |
18 |
— |
— |
— |
— |
|
(140) |
28 |
26 |
26 |
24 |
24 |
22 |
22 |
22 |
21 |
21 |
21 |
21 |
21 |
20 |
— |
— |
— |
|
160 |
32 |
30 |
30 |
28 |
28 |
26 |
25 |
25 |
25 |
24 |
24 |
24 |
24 |
24 |
24 |
24 |
24 |
|
(180) |
36 |
34 |
32 |
32 |
30 |
30 |
28 |
28 |
28 |
28 |
26 |
26 |
26 |
26 |
26 |
26 |
26 |
|
200 |
40 |
38 |
38 |
34 |
34 |
32 |
32 |
32 |
30 |
30 |
30 |
30 |
30 |
30 |
30 |
30 |
28 |
|
(225) |
45 |
42 |
42 |
40 |
38 |
36 |
36 |
36 |
34 |
34 |
34 |
34 |
32 |
32 |
32 |
32 |
32 |
|
250 |
50 |
48 |
45 |
45 |
42 |
40 |
40 |
40 |
38 |
38 |
38 |
38 |
36 |
36 |
36 |
36 |
36 |
|
280 |
55 |
52 |
52 |
50 |
48 |
45 |
45 |
45 |
42 |
42 |
42 |
42 |
42 |
40 |
40 |
40 |
40 |
|
315 |
65 |
60 |
60 |
.55 |
52 |
52 |
50 |
50 |
48 |
48 |
48 |
48 |
45 |
45 |
45 |
45 |
45 |
|
355 |
70 |
70 |
65 |
63 |
60 |
60 |
55 |
55 |
55 |
55 |
55 |
52 |
52 |
52 |
52 |
52 |
52 |
|
400 |
80 |
75 |
75 |
70 |
70 |
65 |
63 |
63 |
60 |
60 |
60 |
60 |
60 |
60 |
60 |
60 |
60 |
|
450 |
90 |
85 |
80 |
80 |
75 |
75 |
70 |
70 |
70 |
70 |
65 |
65 |
65 |
65 |
65 |
65 |
65 |
|
500 |
100 |
95 |
90 |
90 |
85 |
80 |
80 |
80 |
75 |
75 |
75 |
75 |
75 |
75 |
75 |
70 |
70 |
|
560 |
ГОСТ 12289 - 76 предусматривает |
90 |
90 |
90 |
85 |
85 |
85 |
85 |
80 |
80 |
80 |
80 |
80 |
||||
|
630 |
100 |
100 |
100 |
95 |
95 |
95 |
95 |
90 |
90 |
90 |
90 |
90 |
|||||
|
710 |
120 |
110 |
110 |
110 |
110 |
105 |
105 |
105 |
105 |
105 |
105 |
100 |
|||||
|
800 |
130 |
130 |
125 |
125 |
120 |
120 |
120 |
120 |
120 |
120 |
120 |
120 |
|||||
|
900 |
— |
— |
140 |
140 |
140 |
130 |
130 |
130 |
130 |
130 |
130 |
130 |
|||||
|
1000 |
— |
— |
160 |
150 |
150 |
150 |
150 |
150 |
150 |
150 |
140 |
140 |
|||||
70. Формулы и пример расчета конической передачи с прямыми зубьями без смещения
Линейные размеры, мм
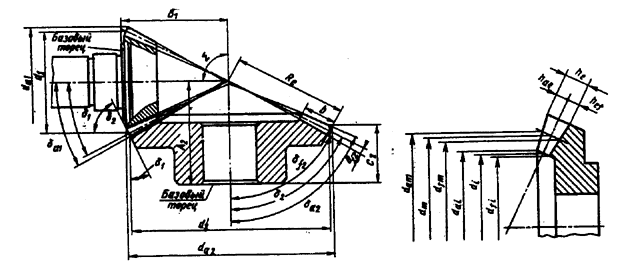 |
|||
| Параметры и обозначения | Расчетные формулы и указания | Численные значения |
|
| Исходные данные |
Число зубьев z1 |
Задаются или выбираются в соответствии с |
18 20 |
|
Внешний окружной |
Определяют из расчета на прочность (при |
5 | |
|
Межосевой угол Внешний торцовый |
По конструктивным соображениям По ГОСТ 13754-81 |
90°
— |
|
|
Число зубьев плоского колеса zc |
26,9072 | ||
|
Внешнее конусное расстояние Re |
Re= 0,5mezc | 67,268 | |
|
Ширина зубчатого венца b |
20 | ||
|
Среднее конусное расстояние Rm |
Rm=Re- 0,5b | 57,268 | |
|
Средний окружной модуль mm |
4,2567 | ||
|
Средний делительный диаметр dm |
dm1=mmz1 dm2=mmz2 |
77,6206 85,1340 |
|
|
Угол делительного конуса δ |
tgδ1= z1/ z2 δ2= 90° - δ1 sinδ1= cosδ2 cosδ1=sinδ2 |
41°59' 48°01' 0,66891 0,74334 |
|
|
Передаточное число u |
u= z2/z1 при u < 2,5 не изменяется толщина зуба исходного контура |
1,1111 | |
|
Внешняя высота головки зуба hae |
hae при h*=1 | 5 | |
|
Внешняя высота ножки зуба hfe |
hfe=hae + 0,2me | 6 | |
|
Внешняя высота зуба he |
he=hae + hfe | 11,0 | |
|
Внешняя окружная толщина зуба se |
se= 0,5πme | 7,85 | |
|
Угол ножки зуба θf |
tg θf = hf /Re; | tg θf = 0,0893; θf = 5°06' |
|
|
Угол головки зуба θa |
θa= θf | 5°06' | |
|
Угол конуса вершин δa |
δa1 = δ1+ θa δa2 = δ2+ θa |
47°05' 53°07' |
|
|
Угол конуса впадин δf |
δf1 = δ1- θf δf2 = δ2- θf |
36°53' 42°55' |
|
|
Внешний делительный диаметр de |
de1= mez1 de2= mez2 |
90 100 |
|
|
Внешний диаметр вершин зубьев dae |
dae1= de1+ 2haecosδ1 dae2= de2+ 2haecosδ2 |
97,4334 106,6891 |
|
|
Расстояние от вершины до плоскости |
B1= 0,5de2 - haesinδ1 B2= 0,5de1 - haesinδ2 |
56,6555 41,2833 |
|
|
Внешняя постоянная хорда зуба ŝc |
ŝce= 0,883se | 6,9315 | |
|
Высота до внешней постоянной хорды ĥce |
ĥce = hae - 0,1607se | 3,7385 | |
|
Половина внешней угловой толщины ψe, |
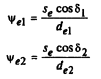 |
0,0648 рад или 3°42'45" 0,0525 рад |
|
|
Внешняя делительная толщина зуба по |
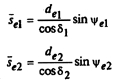 |
7,8340
7,04496 |
|
|
Высота до внешней делительной хорды |
ĥae1 = hae + 0,25ŝe1ψe1 ĥae2 = hae + 0,25ŝe2ψe2 |
5,1272 5,1030 |
|
|
*1 рад = 57°17'44". |
|||
71. Формулы и пример расчета ортогональной конической передачи
с прямыми зубьями при стандартном исходном контуре со смещением
Линейные размеры, мм
|
Параметры и обозначения |
Формулы и указания |
Численные значения |
|
|
Исходные данные |
Число зубьев z1 |
— |
15 |
|
Внешний окружной модуль m, |
— |
5 |
|
|
Внешний торцовый исходный контур |
По ГОСТ 13754-81 |
— |
|
|
Число зубьев плоского колеса zc |
|
33,5410 |
|
|
Внешнее конусное расстояние Re |
Re= 0,5mezc |
83,8525 |
|
|
Ширина зубчатого венца b |
|
25 |
|
|
Среднее конусное расстояние Rm |
Rm=Re- 0,5b |
71,3525 |
|
|
Средний окружной модуль mm |
|
4,2546 |
|
|
Внутренний окружной модуль mt |
|
3,5093 | |
|
Средний делительный диаметр dm |
dm1=mmz1 dm2=mmz2 |
63,8190 |
|
|
Угол делительного конуса δ |
tgδ1= z1/ z2 |
26°34" 0,44724 |
|
|
Передаточное число u |
u= z2/z1 | 2 | |
|
Коэффициент смещения у шестерни x1 |
x1 (по табл. 68) |
0,40 | |
|
Коэффициент изменения толщины зуба |
xτ1 | 0 (так как u < 2,5) |
|
|
Внешняя высота головки зуба hae |
hae1= (h*a+ x1)me hae2= 2h*ame - hae1 |
7,0000 3,0000 |
|
|
Внешняя высота ножки зуба hfe |
hfe1=hae2 + 0,2me hfe2=hae1 + 0,2me |
4,0000 |
|
|
Внешняя высота зуба he |
he1=hae1 + hfe1 he2=hae2 + hfe2 |
11,0000 11,0000 |
|
|
Внешняя окружная толщина se |
se1= (0,5π + 2x1tga +xτ1)me se2=πme - se1 |
9,3096
6,3979 |
|
|
Угол ножки зуба θf |
tg θf1 = hfe1 /Re | tg θf1 =0,04770 θf1 =2°44' |
|
| tg θf2 = hfe2 /Re | tg θf2 =0,09540 θf2 =5°27' |
||
|
Угол головки зуба θa |
θa1 =θf2 θa2 =θf1 |
5°27' 2°44' |
|
|
Угол конуса вершин δa |
δa1 = δ1+ θa1 δa2 = δ2+ θa2 |
32°01' 66°10' |
|
|
Угол конуса впадин δf |
δf1 = δ1- θf1 δf2 = δ2- θf2 |
23°50' 57°59' |
|
|
Внешний делительный диаметр de |
de1= mez1 de2= mez2 |
75,0000 150,0000 |
|
|
Внешний диаметр вершин зубьев dae |
dae1= de1+ 2hae1cosδ1 dae2= de2+ 2hae2cosδ2 |
87,5217 152,6834 |
|
|
Расстояние от вершины до плоскости |
B1= 0,5de2 - hae1sinδ1 B2= 0,5de1 - hae2sinδ2 |
71,8693 34,8168 |
|
| Расчет внешней постоянной хорды и высоты до нее (при x1≤ 0,4) | |||
|
Внешняя постоянная хорды зуба ŝce |
ŝce1= 0,883se1 ŝce2= 0,883se2 |
8,2206 5,6496 |
|
|
Высота до внешней постоянной хорды |
ĥce1 = hae1 - 0,1607se1 ĥce2 = hae2 - 0,1607se2 |
5,5039 1,9718 |
|
|
Расчет внешней делительной толщины зуба по хорде и высоты до нее (при x1≤ 0,4) |
|||
|
Половина внешней угловой толщины ψ |
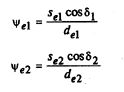 |
0,11102
0,01907 |
|
|
Внешняя делительная толщина зуба по |
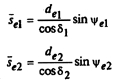 |
9,2986
6,3422 |
|
|
Высота до внешней делительной хорды |
ĥae1 = hae1 + 0,25ŝe1ψe1 ĥae2 = hae2 + 0,25ŝe2ψe2 |
7,2584 3,0305 |
|
72. Дополнительный расчет
Данный расчет приводится в дополнение к табл. 71 в части расчета внешней постоянной хорды, высоты до нее и расчета внешней делительной толщины зуба по хорде и высоты до нее и расчета внешней делительной толщины зуба по хорде и высоты до нее для более общих случаев.
| Параметры и обозначения | Формулы и указания |
| Расчет внешней постоянной хорды зуба и высоты до постоянной хорды* | |
|
Внешняя постоянная хорда зуба ŝce |
ŝce= secos2a |
|
Высота до внешней постоянной хорды зуба ĥce |
ĥce= hae - 0,25sesin2a |
| Расчет внешней делительной толщины зуба по хорде и высоты до хорды | |
|
Половина внешней угловой толщины ψe, рад* |
|
|
Внешняя делительная толщина зуба по хорде ŝe |
|
|
Высота до внешней делительной хорды зуба ĥae |
ĥae= hae + 0,25seψe |
|
* Метод измерения рекомендуется для шестерни при любом значении х1, а для колеса при x1≤ 0,4. |
|
|
ГОСТ 19624—74 предусматривает расчет конической передачи с прямыми зубьями при межосевом угле Σ≠ 90°, а |
|
